공돌이가 되고픈 미생

회로이론은 새로 생성되거나 사라지는 알짜전하는 없다는 것을 가정한다.

이것은 우리가 흔히 알고 있는 키르히호프의 전류법칙(kirchhoff current law) 과 연결된다.

키르히호프 전류법칙

자속보존의 법칙

우리가 전자기학때 배웠던 자속 보존의 법칙을 떠올려보자.

위의 화살표는 벡터(vector) 라는 뜻이고, 가운데 점은 내적(inner product), 앞에 역삼각형 형태는 gradient를 의미한다.

gradient의 내적은 발산(divergence)이다.

따라서, 위의 수식은 자속 밀도 B(magnetic flux density)의 기울기 구배와 내적을 하면 0이라는 뜻이다. 

수학적으로 계산해보면, 벡터 내적 벡터는 스칼라 값이 나온다는 것을 알 수 있다.

아직도 무슨말인지 잘 모르겠다면, 적분형으로 바꾸어 생각해보자.

위의 수식에 부피적분을 취하면 아래의 수식처럼 표현될 수 있다.

발산정리를 통해 enclosed surface 형태로 변환할 수 있으며, 그 값이 오른쪽과 같다.

그럼, 오른쪽 수식의 의미는 무엇일까?

어떤 닫힌 폐곡선 면에 존재하는 자속 밀도를 적분해서 계산을 하면 0이라는 의미이다.

부호의 양(+)는 나가는 방향을 의미하므로, 여기서 키워드는 Net outward flux 이다.

즉, 바깥쪽으로 향하는 flux의 총량을 의미하며, 이 값이 0이라는 의미이다. 

 전하보존의 법칙

앞서 회로이론에서 가정한 것은 전하가 보존된다. 즉, 갑자기 전하가 생기거나 줄지 않는다는 것을 가정했다.

아래의 수식은 전하보존의 법칙의 식이다.

물리 현상을 이해하기 쉬운 것은 적분형으로 고쳐서 생각하는 것이다.

따라서, 위의 수식에서 각각을 적분시켜 생각하면 아래와 같다.

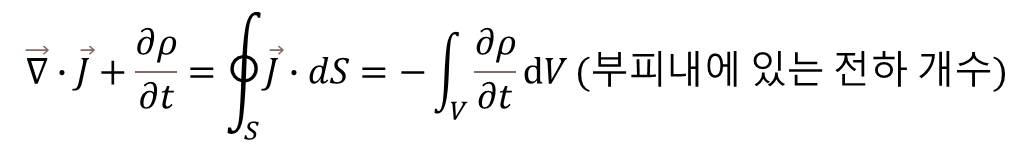
즉, 나가는 전류의 합이 부피내에 있는 전하가 사라진 것과 같다는 말이 된다.

아래 예제를 통해 생각해보자.

예제문제

위의 회로에서 각각 부품에 흐르는 전류를 키르히호프 전류 법칙을 이용해 구한다고 생각해보자.

그럼, node A 점에서 동그란 원형의 면적을 잡고, 위에서 학습한 키르히호프 전류 법칙에 의해 나가는 전류의 총합이 0이다.

그럼, 6V 쪽으로 흐르는 전류, 저항 2옴에 흐르는 전류, 저항 3옴에 흐르는 전류를 0이라고 하면 V=IR 이므로 아래와 같은 식을 세울 수 있다.

ia는 6V 쪽으로 흐르는 전류를 임의로 지정했고, Va는 node A의 전압을 의미한다.

이때, Va는 전원 6 V에 의해 6으로 설정되어 있으므로, 미지수가 1개인 식이 되어 쉽게 풀 수 있다.

따라서 ia= - 5 A 이다.

여기에서 음수는 전류의 방향이 반대라는 것을 의미하므로, 6 V에서 흐르는 전류는 위의 노란색에서 표시한 것(오른쪽->왼쪽)이 아닌 왼쪽에서 오른쪽으로 흐르는 것을 알 수 있다.

회로이론의 두번째 가정은 집중정수계를 가정한다.

실제, 우리가 실생활에서 접하는 상황은 분포정수계이다.

하지만 기초를 배우는 회로이론에 있어서 바로 분포정수계를 이용해 학습하면, 학습하는데 있어 큰 산을 넘어야 한다.

그래서 회로이론은 집중정수계를 가정한다.

따라서, 전파효과가 매우 작거나 무시가 된다.

그럼, 어떻게 집중정수계와 분포정수계를 구분할 수 있을까?

집중정수계(lumped parameter system)

집중정수계와 분포정수계를 이해하는 방법은 강체(rigid body)와 순두부를 떠올려 비교하면 된다.

강체는 하나의 질점으로 표현이 가능하며 물체의 두 점의 상대적인 위치가 변하지 않는다.

따라서, 강체를 계산할 때에는 하나의 질점만 계산하면 되지만 순두부는 각 질점 하나하나를 계산해서 더해야하는 느낌이다.

우리는 공학생이다. 그럼 어떻게 수치적으로 집중정수계인 것을 알 수 있을까?

어떤 물체를 F라는 힘으로 쳤을 때, 상대편으로 도달하는 시간을 통해 집중정수계인지 알 수 있다.

도달하는 지연시간을 Δt 라고할 때, 이는 Δt=l/v (거리=시간 × 속도 이니까) 로 표현할 수 있다.

이때, 입력하는 힘 대신 한주기 T의 sine 파의 전원을 입력을 가정했을 때, Δt/T << 1 이면 집중정수계이다.

그럼 속도는 어떻게 측정할 수 있을까? 강체의 속도는 다음과 같이 표현할 수 있다.

v: 신호의 전달속도, E:탄성률(yong's modulus, 이 값이 클 수록 단단한 물질),  ρ : 밀도

그래서 나중에 우리가 실험실에서 사용하는 전원 주파수는 kHz로 실험하는 이유다.

1)만약, MHz면 주기가 급격히 짧아지기 때문에 지연시간 Δt/T << 1 가 만족되지 않으면서 집중정수계가 아니기 때문에 이론적으로 학습한 것과 다른 값이 측정될 수 있다.

2) 혹은 system 크기가 작아지면,  Δt=l/v   식에서 l이 급격하게 작아지게 되면서 Δt 가 작아진다. 그래서, Δt/T << 1 가 만족되지 않으면서 집중정수계가 아니다.

회로이론은 집중정수계 시스템을 가정하고 학습하는 것을 잊지 말자.

회로이론은 몇가지 가정을 통해 회로 해석(analysis)하는 것을 목적으로

회로 설계(design)에 대한 능력을 함양하기 위해서 공부한다.

따라서, 회로이론은 몇가지 가정을 통해 회로를 단순화한다.

그 중 첫번째는 선형 시스템만 가정해 공부한다.

일반적으로 선형시스템(linear system)을 가정하는 이유는 수학적으로 해석하기가 쉽기 때문이다.

선형시스템(linear system)

선형시스템은 2가지 조건이 만족될 때 선형시스템이라 부를 수 있다.

1) 정수배

: a -> i 일 때, ka -> ki 를 만족한다.

2) 중첩(superposition)

: i1->v1, i2->v2 일 때, => i1+i2 -> v1+v2

각각의 예를 들어서 학습해보자.

정수배 예)

가령, 6 V 전원에 1 kΩ 저항이 연결되어 있다고 가정해보자.

그렇다면, 이 회로의 전류는 6 mA가 흐른다.

그럼 12 V 전원에 6 mA가 흐르려면 저항이 얼마나 커야할까?

V=I × R 이므로, I가 동일하다면 2V=I × 2R 이 만족한다.

따라서, R=2 kΩ 이 되는 것이다.

이 때,  V가 2배가 되었을 때, R이 2배이다. 

즉, k배 했을 때 동일한 값을 얻을 수 있는 이러한 것이 정수배가 가능한 것을 의미한다.

중첩 예)

위의 회로가 있다고 가정해보자. 

그럼 저항에 흐르는 전류는 얼마일까?

왼쪽 회로에 흐르는 전류를 i1, 오른쪽에 흐르는 전류를 i2 라고 가정해보자. 그럼 식 2개를 세울 수 있다.

(i1-i2) × 1k = 6 V     (식1)

i2 = - 2 A                  (식2)

따라서, i1= 6mA - 2 A = -1.994 mA

그럼 중첩의 정리를 이용해서 계산해보자.

우선, 오른쪽의 전원이 0이라고 가정해보자.

전류원이 0 A 라는 의미는 회로적으로는 open 즉 회로가 끊어진 것이다.

따라서, 저항에 흐르는 전류는 6 m A 이다.

이번엔 반대로 왼쪽 전원이 0이라고 가정해보자.

전압원이 0 V 라는 의미는 회로적으로 short 즉 회로가 연결된 것이다.

따라서, 2 A 전류는 저항에 흐르지 않고 모두 왼쪽으로 흐르는 것을 알 수 있다.

종합하면, Va 라는 node (마디)  의 왼쪽에서 흐르는 전류는

왼쪽으로 2 A, 오른쪽으 6 mA가 흐르기 때문에 더하면 왼쪽으로 1.994 mA가 흐르는 것을 알 수 있다.

이 결과는 처음 i1, i2 라는 전류가 흐른다는 것을 가정해 푼 결과와 같다.

i1 = - 1.994 mA (i1이 오른쪽으로 흐른다고 가정했으므로, - 부호의 의미는 반대로 흐른다는 의미이다.)

수학적으로 i1->v1, i2->v2 일 때, => i1+i2 -> v1+v2 로 푼 결과와 같은 것을 알 수 있다.

결론적으로, 회로이론을 해석할 때에는 해석하고자 하는 시스템이 선형 시스템임을 잊지 말자!!

근처에 있는 휴대폰을 보자. 끊임없이 기지국과 통신하고 있다. (전파를 이용해 에너지가 전달되고 있는 과정)휴대폰 안에 있는 배터리로 휴대폰을 사용할 수 있다. (배터리 안에 저장된 에너지로, 휴대폰을 구동하는 과정)

이 모든 일은 전기전자공학의 예이다.

그럼 어떻게 에너지들이 이동하는 것을 알 수 있을까?

포인팅 벡터 (ponyting vector)

(단위시간당 단위면적당 에너지의 흐름)

벡터이기 때문에 크기와 방향이 있다.

따라서, 전기장의 방향과 자기장의 방향을 알 수 있다면 에너지가 어떻게 전달되고 있는지 알 수 있다.

아래의 그림을 보면서 이해해보자.

만약 전기장 방향이 오른쪽, 자기장 방향이 위라면, 벡터의 외적 곱에 의해 포인팅 벡터는 앞으로 나오는 방향(모니터를 뚫고 나오는 방향)이 된다.

그럼, 왜 포인팅 벡터는 단위시간당 단위면적당 에너지의 흐름이 되는 것인가?

이럴땐 단위를 살펴보면 이해하기 쉽다.

전기장세기(electric field intensity) : V/m

자기장세기(magnetic field intensity) : A/m

따라서, 포인팅 벡터 는 가 된다.

여기서 VA는 W 이므로, W=J/s 로 변환할 수 있다.

최종적으로, 포인팅 벡터는 단위시간당 단위면적당 에너지를 의미한다.

따라서, 포인팅 벡터를 구한다는 의미는 에너지가 어떻게 전달되고 있는지 크기와 방향을 알 수 있기 때문에 에너지의 흐름을 알 수 있다.

다음 예를 통해 포인팅벡터를 생각해보자.

에너지흐름 생각해보기 - 예)동축케이블

위에 보이는 선은 흔히 볼 수 있는 동축(co-axial) 케이블이다. 동축케이블에서의 동축이라는 뜻은 구리동이 아닌 같을 동자를 사용하고 있다. 즉 중심에 있는 구리와 같은 도체와 바깥쪽으로 있는 접지의 축이 같다는 말에서 따온 것이다.

그래서 영어도 co-axial 이다. 이를 도식화하면 아래 그림과 같다.

원통형 바깥쪽은 바깥쪽 축은 0 V(접지, 바깥쪽 검은색 원통형 라인)이고, 구리선에 내부 신호가 인가된다(가운데 주황색 선).

그래서 내부 신호가 인가되는 부분과 바깥쪽 축 방향으로 방향이 생긴다. (가장 왼쪽 원통형 표면, 검은색 화살표)

신호가 인가되는 부분(주황색 선)에서 전류 i 가 흐르므로, 오른나사 방향이 방향이다. (앙페르 오른쪽 나사 법칙, 가장 오른쪽 파란색 화살표 참조)

이를 벡터곱을 해 포인팅벡터를 구해보면 도선 축이 아닌 사이방향에 포인팅벡터 가 발생함을 알 수 있다. (가운데 초록색 화살표)

• 그래서 일반적으로 에너지가 가운데 도선을 타고 간다라고 생각하기 쉬운데 실제로는 가운데 도선(주황색선)과 0 V 로 접지된 선(검은색 원통형 가장 바깥쪽)사이의 내부 공간으로 에너지가 이동한다!!!!***

그래서 이 내부 공간에 채워진 물질에 따라 에너지 효율이 달라지기 때문에 내부에 채워져 있는 물질 또한 매우 중요함을 알 수 있다.

에너지흐름 생각해보기 - 예) 기본회로

아래 회로는 6 V 전원에 연결된 저항 소자를 간략히 그린 그림이다.

실제로 윗쪽선은 6 V 전원에 의해 6 V 가 인가되어 있고, 아랫쪽 선은 접지로 연결되어 있다. 전류는 초록색 화살표처럼 흐르고 있다. 그렇다면 에너지는 어떻게 전달될까?

위에서 말했던 것처럼 에너지가 도선을 타고 전달된다라고 생각하기 쉽다.

(전기장의 세기) 와 (자기장의 세기) 를 생각해보자.

전기장의 세기는 6 V 와 0 V 밖에 없으로 위에서 아래방향인 전기장 세기를 확인할 수 있다.

자기장의 세기는 전류의 흐름을 먼저 생각해야한다.

전류의 방향은 초록색 화살표 방향으로 흐르고 있으므로, 오른나사로 생각하면 들어가는 방향과 나오는 방향이 다음 그림과 같다.

따라서 (포인팅벡터) 는 전기장 세기와 자기장 세기의 곱이므로 아래그림처럼 표현할 수 있다. 

즉, 에너지 흐름은 도선을 따라서 흐르는 것이 아닌 공간을 타고서 화살표 방향처럼 흐르는 것이다.

이번 글에서는 에너지의 흐름을 표현하는 포인팅 벡터에 대해서 알아보았다.